재귀함수를 이용한 피보나치를 구현해 보고
동적프로그래밍을 활용하여 쉽게 설명할 수 있는 예제인 피보나치 수를 소개한다.
그리고 동적프로그래밍이 무엇이고 이점이 뭔지 살펴보려 한다.
예제 문제
https://www.acmicpc.net/problem/10870
10870번: 피보나치 수 5
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
피보나치 수 정의

피보나치의 수를 구한다고 가정할 때 다음과 같이 나타낼 수 있다. (예시에서는 fib(5))
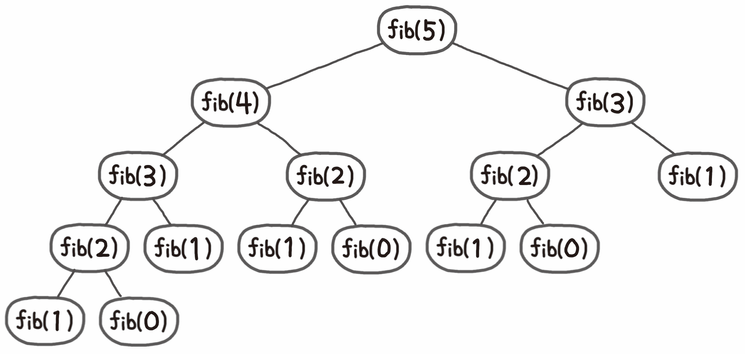
피보나치 수열은 재귀함수 형태로 표현된다.
pseudocode
f(0) = 1
f(1) = 1
f(n) = f(n-1) + f(n-2) when n > 1
재귀함수 풀이
그런데 재귀함수 방식으로 컴퓨터가 계산하면 비효율적이다.
Java
import java.util.Scanner;
public class Fibo {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println(fibo(sc.nextInt()));
}
static int fibo(int n) {
if(n == 0) {
return 0;
}
else if(n == 1 || n == 2) {
return 1;
}
else {
return fibo(n-1) + fibo(n-2);
}
}
}Python
n = int(input())
def pi(n):
if n==0:
return 0
elif n== 1 or n==2:
return 1
else:
return pi(n-1)+pi(n-2)
print(pi(n))왜냐하면 재귀함수 방식으로 계산하면 피보나치 수 5를 구할 때 총 15번의 함수 호출을 해야 하는데
피보나치의 수를 100, 또는 1000.. 같이 피보나치의 수가 높아질 수록 수많은 함수 호출과 연산을 수행하여야 한다.
(fib(1)(2)...(n-1)까지의 연산결과를 알고있음에도...)
매우 비효율적이다
이때 시간복잡도는 O(2^N)이다..
이를 해결하기 위해 동적계획법 이라는 알고리즘 설계 기법이 나온 것이다.
불필요한 반복계산을 막기 위해 이전에 함수호출을 통해 계산한 값들을 배열에 저장해서 효율적으로 값을 구하는 방식이다.
동적 계획법은 크게 Top-down 방식과 Bottom-up 방식이 있다.
Top-down
Top-down은 큰 문제부터 시작해서 계속 작은 문제로 분할해 가면서 푸는 것.
fibo(4)를 구하는 큰 문제는 fibo(3), fibo(2)를 구하는 작은 문제로 나눌 수 있고 fibo(3)은 fibo(2), fibo(1)을 구하는 더 작은 문제로 나눌 수 있음
이를 다음과 같이 구현할 수 있다.
Java
public class FiboDP {
public static int[] memo;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
memo = new int[n+1];
System.out.println(fibo(n));
}
public static int fibo(int i) {
if (i == 0) {
return 0;
} else if (i == 1 || i == 2){
return 1;
}
if(memo[i] != 0) {
return memo[i];
}
memo[i] = fibo(i-1) + fibo(i-2);
return memo[i];
}
}
Python
n = int(input())
d = [0] * (n+1)
def pibo(n):
if n == 0:
return 0
elif n == 1 or n == 2:
return 1
if d[n] != 0:
return d[n]
d[n] = pibo(n-1) + pibo(n-2)
return d[n]
print(pibo(n))
Bottom-up
작은 문제부터 시작해서 작은 문제를 점점 쌓아 큰 문제를 푸는 것.
첫 번째 피보나치 수와 두 번째 피보나치 수를 구하면 세 번째 피보나치 수를 구할 수 있고, 두 번째, 세 번째 피보나치 수를 구하면 네 번째 피보나치 수를 구할 수 있다.
Java
import java.util.Scanner;
public class FiboDP2 {
public static int[] memo;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
memo = new int[n+1];
if(n == 0) {
memo[0] = 0;
} else if(n == 1) {
memo[1] = 1;
} else if(n == 2) {
memo[2] = 1;
} else {
memo[0] = 0;
memo[1] = 1;
memo[2] = 1;
for (int i = 3; i < n+1; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
}
System.out.println(memo[n]);
}
}
Python
n=int(input())
d=[0]*(n+1)
if n==0:
d[0]=0
elif n==1:
d[1]=1
elif n==2:
d[2]=1
else:
d[0]=0
d[1]=1
d[2]=1
for i in range(3,n+1):
d[i]=d[i-1]+d[i-2]
print(d[n])
DP로 구현하면 O(N)의 시간복잡도를 가진다.
'Problem Solving > Algorithm' 카테고리의 다른 글
| [알고리즘] Palindrome 알고리즘 - 파이썬 (0) | 2022.05.13 |
|---|---|
| [알고리즘] 누적합 알고리즘 (0) | 2022.05.13 |
| [알고리즘] 이진 탐색 (Binary Search) (0) | 2022.05.11 |
| [알고리즘] 정렬 (선택, 버블, 삽입, 퀵, 머지, 계수) (0) | 2022.05.10 |
| [알고리즘] DFS/BFS - 파이썬, 자바 (0) | 2022.03.25 |
